
| 5. Isaac Newton (1642-1727) |  |
Nous savons tous que c'est Newton, qui, au travers d'une des plus grandes oeuvres scientifiques de tous les temps : "Principia", donne la première expression de la force de gravitation, et fonde en même temps toute la mécanique, science des mouvements des corps. Nous allons voir comment sa découverte s'inscrit dans la continuité des travaux des post-coperniciens.
Newton est né en Angleterre en 1642 et a fait ses études à Cambridge, sans être un étudiant particulièrement remarqué. Il devient assistant à Trinity College en 1667, et à cette époque on enseignait la physique Cartésienne. Cette conception tout à fait nouvelle du monde était encore à peine tolérée. De manière simplifiée, Descartes (cf. cours de philo) défendait l'idée d'un monde entièrement mécanique, géométrique. Seule la matière en mouvement le constituait. Descartes a même proposé un modèle de formation du système solaire, plus tard corrigé par Kant, mais qui préfigure les modèles modernes. Même si le système cartésien n'était pas performant en termes de prévisions, car il était avant tout descriptif et qualitatif, avec la pensée cartésienne était née l'idée que le monde est intelligible et que c'est par les sciences mathématiques que nous pourrons le comprendre.
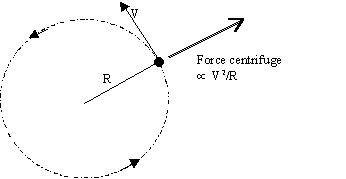
Newton commença par travailler sur le modèle d'orbites planétaires, proposé par Descartes, qui expliquait qualitativement le mouvement circulaire des planètes comme un équilibre entre une force attractive vers le Soleil et une force répulsive, par analogie avec une pierre qui tourne attachée par une corde à un axe. Nous savons aujourd'hui que cette force répulsive, dite "centrifuge" est en fait une force inertielle, c'est à dire, une conséquence du changement de repère (ici repère tournant), elle n'est en rien liée à la gravitation. C'est cependant en suivant cette idée un peu fausse d'une force répulsive que le physicien anglais Robert Hook aura le premier l'idée d'une force en 1/r2, mais ce sera Newton qui saura en exploiter les conséquences et comprendre le mouvement des planètes.
| Le
physicien Huygens avait calculé la force dirigée vers l'extérieur
qui s'exerce sur une pierre qui tourne autour d'un axe. Il avait montré
que cette force était proportionnelle au carré de la vitesse,
divisé par le rayon (V2/R). Sur la base de cette idée,
Hook a voulu calculer ce que cela donnait pour une planète
: on sait par la troisième loi de Kepler que le carré de
la période de révolution d'une planète (autour du
soleil) est proportionnel au cube du rayon de son orbite ( kr3).
|
 |
En 1679, alors que Newton se débattait encore avec la théorie cartésienne des forces attractives et répulsives, il reçoit une lettre de Hook (avec lequel s'était déjà engagé une vive polémique sur la nature de la lumière) lui soumettant l'idée suivante : le mouvement circulaire des planètes pourrait sûrement s'expliquer comme la conséquence d'une unique force attractive en 1/r2 qui attire le corps vers le Soleil, mais le mouvement circulaire lui-même est la conséquence de la tendance du corps à conserver un mouvement rectiligne (conséquence du principe d'inertie). Ce mouvement rectiligne est à tout instant modifié par la force attractive et le bilan de ces deux effets est un mouvement circulaire.
Newton qui n'appréciait pas beaucoup Hook, lui proposa une solution mathématique, dans laquelle il fit une erreur, que Hook vit rapidement. Fatigué de ses disputes avec Newton, Hook abandonna finalement l'hypothèse. Cependant Newton, sans le faire savoir, résolut secrètement le problème. En réalité Newton alla beaucoup plus loin que le simple cas d'un mouvement circulaire, et ainsi développa sa théorie de la gravitation universelle et de la mécanique, qu'il publia en 1687 dans son ouvrage, les "principia".
5.1 La gravitation universelle et l'expérience de la pomme
Newton, avant de se plonger complètement dans la description d'une loi en 1/r2, dut d'abord s'assurer expérimentalement de la véracité de cette loi. C'est l'origine de la célèbre histoire de la pomme qui tombe, contée par Voltaire. Le raisonnement de Newton, inspiré de philosophie cartésienne était le suivant : si on suppose qu'une force attractive existe entre le Soleil et les planètes, elle devrait exister entre tout corps constitué de matière. En particulier entre la Terre et la Lune, et entre la Terre et n'importe quel objet à sa surface. On savait déjà à l'époque que la distance Terre-Lune était à peu près de 60 rayons terrestres. Donc la force d'attraction qui s'exerce sur la Lune est (1/60)2 plus petite que celle qui s'exerce sur un corps en chute libre à la surface de la Terre. Maintenant, comment comparer la chute d'un corps sur la Terre et le mouvement de la Lune ? Plaçons-nous à un instant T0 où la Terre, la pierre et la Lune sont alignées sur une même droite D.
Mais alors, pourquoi certains corps chutent-ils et d'autres tournent-ils ? Voici l'explication qu'apporte Newton. On ne l'explique pas autrement aujourd'hui ! Imaginons un canon à la surface de la Terre qui tire des boulets en ligne droite parallèlement au sol. Plus la vitesse initiale du boulet est grande, plus il retombe loin. Appelons L cette distance. Un boulet tiré, commence par parcourir une ligne droite dans l'alignement du fût du canon, puis progressivement s'en éloigne car il chute vers le sol.
 Un
boulet tiré avec une faible vitesse initiale retombe sur le sol
rapidement
Un
boulet tiré avec une faible vitesse initiale retombe sur le sol
rapidement
 |
Un boulet tiré avec plus de puissance tombe plus loin. L'effet de courbure de la terre commence a être visible. |
Maintenant considérons le cas d'un boulet tiré avec une TRES grande vitesse initiale. Comme prévu, il commence par suivre la ligne de tir puis progressivement s'en éloigne pour chuter. Mais il nous faut considérer le phénomène suivant : étant donné qu'il parcourt une très grande distance avant d'atteindre le sol il va voir le sol s'éloigner de lui ! Parce que la Terre est ronde et si vous vous déplacer dans l'air suivant une exacte ligne droite, inévitablement vous vous éloignez du sol, puisqu'il est COURBE. Suivant ce raisonnement, si le boulet est tiré suffisamment vite, il est possible que le sol s'éloigne plus vite du boulet (du fait de la courbure de la Terre) qu'il ne chute vers le sol. Dans ce cas le boulet n'atteindra jamais le sol et partira dans l'espace. Sous certaines conditions, il est satellisé autour de la Terre, sinon, il est éjecté dans l'espace et se sépare complètement de la Terre.
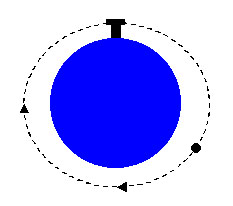 Un boulet tiré à très grande vitesse se satellise.
Un boulet tiré à très grande vitesse se satellise.
La Lune est par conséquent un corps qui chute constamment vers la Terre, mais étant donné sa vitesse et son éloignement, elle n'atteint jamais la Terre qui se dérobe constamment. Elle adopte un mouvement circulaire autour de la Terre car la force de gravitation l'oblige quand même à suivre la Terre dans son mouvement. Il en est de même pour le mouvement des planètes par rapport au Soleil. Enfin, c'est là le dernier coup porté à la physique d'Aristote : les lois qui régissent le mouvement des objets célestes sont les mêmes sur Terre ! Il n'y a plus de séparation en monde Terrestre et Céleste !
Dans les Principia, Newton ne se contente pas de relater cette expérience et d'exposer la loi en 1/R2. Il développe tout d'abord les fondements de la mécanique, et expose ensuite la gravitation universelle. De plus pour venir à bout des calculs, il développe une méthode mathématique ancêtre du calcul différentiel, dite méthode des fluxions.
Dans son ouvrage, Newton commence par exposer ses 3 lois du mouvement qui fondent la mécanique. Elles s'énoncent comme suit :
1ère loi :
Tout objet en état de mouvement rectiligne uniforme et soumis à aucune force extérieure, conserve son mouvement, dans un repère galiléen.
Cette loi est la reformulation du principe d'inertie formulé par Galilée. On l'appelle couramment "Le principe d'inertie"
2ème loi :
La relation entre la force (F) appliquée à un corps et son accélération (a, définie comme la dérivée seconde du mouvement par rapport au temps) s'écrit :
C'est la plus puissante des trois lois, car elle permet de calculer quantitativement le mouvement des corps. De plus, on remarquera que si F=0, alors a=0, on retrouve alors première loi.
C'est aussi une révolution comparée à la physique d'Aristote, qui lui supposait que la force s'exerçant sur un corps est proportionnelle à sa vitesse, et non à son accélération.
3ème loi :
Tout corps soumis à une force exerce en retour une force de même intensité et de direction opposée.
C'est pour cela que l'on tient sur le plancher sans passer au travers !
C'est sur la base de ces trois lois, auxquelles Newton ajoute la force de gravitation qu'il déduit les mouvements des planètes.
Comment écrire cette force ? Tout d'abord, et c'est là le postulat fondamental, elle est en 1/R2 (confirmée par l'expérience de la lune). De plus, on suppose qu'elle est proportionnelle à la masse du corps central, M, car les corps les plus lourds attirent plus fortement les corps les plus faibles. C'est pour cela que la pomme n'a pas beaucoup d'influence sur la Terre car elle l'attire avec trop peu d'intensité.
On peut dans un premier temps écrire la force de gravitation : F= k M/R2 où k reste à déterminer.
Dernière contrainte fondamentale : on a vérifié expérimentalement (avec les expériences de chute des corps faites par Galilée) que l'accélération subie par un corps ne dépend pas de sa masse, c'est pour cela que tous les objets tombent à la même vitesse sur Terre.
Utilisons maintenant la 2ème loi de Newton : F=m a , où m est la masse du corps qui est attiré (la Lune, la Pomme) : On a donc F=ma=k M/R2 => a= kM / mR2.
Cette expression dépend explicitement de m, or on a dit plus haut que l'accélération ne doit pas dépendre de m, ainsi, il faut que k soit proportionnel à m. On écrit alors k= G m, où G est la constante de Gravitation universelle.Ainsi, on a : a=GM/R2. La force de gravitation universelle s'exprime finalement ainsi :
G a pu être mesuré expérimentalement, et vaut : 6.67259 10-11 m3 kg-1.s-2
C'est là, la synthèse de mille années de recherches, de controverses et d'affrontements philosophiques qui contrastent avec l'extraordinaire simplicité de cette expression. De quoi donner le vertige. Il n'est pas interdit de rester quelques secondes à la contempler.
On peut remarquer tout d'abord que c'est une loi symétrique : la force exercée sur le corps de masse m sur celui de masse M est la même que celle exercée par le corps de masse M sur celui de masse m. Mais alors, pourquoi la Terre ne ressent-elle pas l'attraction de la pomme (puisque la pomme ressent bien celle de la Terre) ? Attention ! Il ne faut pas confondre la force et l'accélération. Ce que nous voyons expérimentalement, c'est l'accélération, c'est à dire comment un objet est perturbé dans son mouvement. L'accélération à laquelle est soumise la terre à cause de la Pomme est (comme plus haut) a=Gm/R2 où m est la masse de la pomme c'est à dire ~ 0.01 Kg, or G ~10-11 (G est extraordinairement faible !) et R~106 M (à la surface de la Terre), on à donc a~10-7 m/s2 ce qui est totalement négligeable.
En revanche la pomme est soumise à l'accélération suivante : M~1024 kg, on a donc a~10 m/s2 (en fait plutôt 9.81), l'accélération à laquelle est soumise la pomme est 108 fois plus grande que celle de la Terre ! !
On montre aisément a partir de l'expression de la force de gravitation, illustré ici dans le cas Terre-Soleil:
Qu'est ce que le poids par rapport à la masse ? On dit souvent qu'un corps dans l'espace n'a plus de poids mais, il a toujours une masse. Le poids c'est l'accélération à laquelle est soumis un objet dans un champ de gravitation. C'est, à la surface de la Terre, 9.81 x masse. Si on est suffisamment loin de la Terre et du système solaire pour qu'il n'y ait quasiment plus de champ de gravitation, cette accélération est nulle, et donc l'objet n'a plus de poids. Ce que mesure une balance, c'est cette accélération.
5.3.1 Masse inertielle et masse pesante
C'est là un problème avant tout sémantique :Un fait qui peut intriguer dans l'expression de la force de gravitation. Ecrivons le principe fondamental de l'accélération exercée par un corps de masse M2 sur un corps de masse M1 :
F=M1a (PFD), F= G M1 M2 / R2 (gravitation), d'où :
M1 a = G M1 M2 / R2
A gauche du signe "=" la masse M1 désigne, comme l'avait compris Galilée, une mesure de l'inertie du corps, c'est en quelque sorte sa résistance à se mettre en mouvement : plus M1 est grand, et plus il sera difficile de mettre ce corps en mouvement.
A droite du signe "=" cette même masse M1 est la mesure de l'intensité avec laquelle ce corps attire gravitationellement les autres corps.
Il est intriguant que M1, qui désigne
la même grandeur physique, a des significations différentes
selon qu'on l'inclut à gauche dans l'expression du principe d'inertie,
ou à droite, dans l'expression de la force de gravitation. N'oublions
pas que si M1 apparaît dans la force de gravitation, c'est par une
vérification expérimentale (voir plus haut), qui, comme toute
vérification empirique, est une approximation.
Cette différence sémantique entre M1 dans le principe d'inertie et M1 dans la force de gravitation, a mené les scientifiques à distinguer deux types de masses. On appelle Masse inertielle la masse qui apparaît dans le principe fondamental à gauche du signe "=" et Masse pesante celle qui apparaît dans l'expression de la force de gravitation, à droite du signe "=".
Ces deux masses sont expérimentalement les mêmes, ce qui peut rendre cette distinction apparemment gratuite. Cependant, cette distinction aura une importance fondamentale pour l'établissement des lois de la gravitation générale (principe d'équivalence), car Einstein postulera comme un principe fondamental que les masses inertielles et pesantes sont les mêmes.
A l'époque de Newton, on avait déjà relevé ce fait intriguant, mais ses conséquences se plaçaient alors uniquement sur un plan philosophique, qui n'avaient que peu d'incidence sur le plan scientifique.
5.3.2 Les orbites des planètes du système solaire.
Explorons maintenant quelques-unes des conséquences de la force de gravitation, en particulier en ce qui concerne le mouvement des planètes.
Tout d'abord il faut bien comprendre que le mouvement des planètes est la résultante d'un équilibre entre deux phénomènes :
En résolvant mathématiquement l'équation : m a = GMm/R2 (résolution non triviale) Newton a tout d'abord retrouvé et corrigé les trois lois de Kepler. Il doit en premier lieu se livrer à une approximation avant de comprendre le mouvement des planètes. En effet, nous savons maintenant que tous les corps s'attirent entre eux, en particulier le Soleil et les planètes, mais, il ne faut pas l'oublier, les planètes entre elles ! Cependant, les planètes étant tellement plus légères que le Soleil, leur attraction mutuelle peut être en première approximation négligée. Cette approximation couramment utilisée est appelée "approximation à deux corps".
Dans ce cadre, Newton retrouve les trois lois de Kepler comme des conséquences directes de l'expression de Fg (Fg= force de gravitation). Il les reformule maintenant en ces termes :
1ère loi de Kepler : Les orbites des planètes sont des ellipses dont le Soleil occupe l'un des foyers.
En fait, dans le système solaire, les orbites des planètes sont souvent quasiment des cercles ; le cercle étant un cas particulier d'ellipse. Les comètes par contre ont très souvent des orbites très elliptiques.
2ème loi de Kepler : La ligne qui joint le centre de la planète et celui du Soleil balaie une surface égale en des temps égaux.
Cette loi est valable aussi bien pour les orbites circulaires qu'elliptiques.
3ème loi de Kepler : La relation qui lie la période P des orbites et le demi-grand axe, a, (la distance moyenne entre le Soleil et la planète) est : P2/a3 = 4p 2/G(Mp+Ms), où Ms est la masse du Soleil et Mp la masse de la planète.
Cette loi est légèrement différente de celle qu'avait établit Kepler ( P2/a3 = constante pour toutes les planètes). En effet, Newton donne la valeur de cette constante, de plus, il montre qu'elle n'est pas, justement, constante : elle dépend de la masse Mp de la planète. Kepler qui a déterminé cette loi par observations ne pouvait pas deviner cette dépendance en Mp. En effet, Mp est toujours négligeable devant Ms, ainsi P2/a3~4p 2/GMs (Jupiter, la plus massive des planètes, est mille fois plus légère que le Soleil), ce qui explique que d'une planète à l'autre, Kepler n'a pu voir de différence dans la valeur de cette constante.
5.3.3 Equation de L'orbite
Deux corps en interaction gravitationnelle décrivent tous deux une orbite autour de leur centre de gravité. L'orbite la plus simple est l'ellipse. Dans le cas où un des deux corps est de masse négligeable face à l'autre (c'est le cas des planètes comparées au Soleil), alors le gros corps peut être considéré comme à peu prés fixe, et dans certains cas, le petit corps décrit quasiment un cercle autour du plus gros.
L'ellipse et le cercle ne sont pas les seules orbites possibles : elles sont au nombre de quatre et appartiennent à une famille de courbes bien connues depuis longtemps : les coniques.
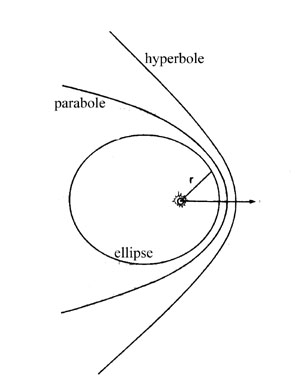
| Les
coniques sont les courbes que l'on obtient en coupant un cône avec
un plan. On obtient le cercle, l'ellipse, la parabole et l'hyperbole. Ces
courbes sont caractérisées par une grandeur positive appelée
excentricité, notée e, qui caractérise plus
ou moins l'extension spatiale de l'orbite : si e =0 c'est un cercle, si
0<e<1 c'est une ellipse. Le cercle et l'ellipse sont des courbes
fermées. Enfin si e=1 c'est une parabole, si e >1 c'est une hyperbole.
Ces deux dernières orbites sont des courbes ouvertes.
|
 |
L'équation de la trajectoire s'écrit : R= k2/m (1+e Cos(f) ) Où k est le moment angulaire = R vectoriel R' (R'= dR/dt)
m est : G(Ms+Mp)
e est l'excentricité
f est appelé l'anomalie vraie, c'est l'angle (Planète, Soleil, Périhélie) où le Périhélie est le point où la planète est le plus proche du Soleil. L'orbite de quelques planètes est presque circulaire (e <<1), par exemple Vénus, c'est aussi le cas des satellites que l'on met en orbite autour de la Terre. La distance avec le corps central est toujours constante. Cependant, en général, les planètes ont des orbites elliptiques avec de petites excentricités, mais bien mesurables (0.25 pour Pluton, 0.08 pour Mars, 0.017 pour la Terre). C'est aussi le cas des comètes qui ont souvent une forte excentricité (proche de 1). Certaines comètes ont des orbites paraboliques (e=1), ce qui signifie qu'elles passent au voisinage du Soleil qu'une unique fois, quittent le Système Solaire et s'en vont à l'infini. Enfin, les trajectoires hyperboliques se rencontrent dans le cas de l'interaction gravitationnelle entre deux étoiles qui se croisent dans l'espace.
Le calcul de la position de la planète sur son orbite est assez complexe, et nous reportons les équations ici uniquement pour mémoire . Nous raisonnons dans le cas d'une ellipse, mais ces résultats se prolongent sans problème au cas des orbites paraboliques et hyperboliques.
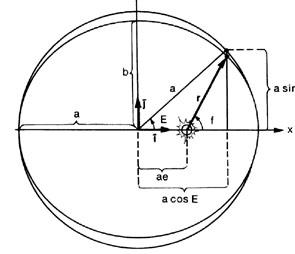
Soit E l'angle entre le centre de l'ellipse, le Soleil et la position projetée de la planète sur le cercle circonscrit à l'ellipse, voir le dessin (E est appelé anomalie excentrique). Connaître la position de la planète sur son orbite, c'est connaître E.
| L'équation
du mouvement est :
E - e Sin(E)=M où M=2p t/P (anomalie moyenne) (P = période de révolution)
|
 |
Cette équation est appelée "l'équation de Kepler", elle donne la position de la planète sur sa trajectoire. Elle n'a pas de solution analytique simple, elle se résout donc numériquement. Dans le cas d'une orbite circulaire, les anomalies vraies, excentriques et moyennes (soient les angles f, E et M) sont égales. Pour calculer la période de révolution, on utilise la vitesse moyenne de rotation donnée par w =(GM/R3)1/2 où G est la constante de gravitation, M la masse du corps central et R est la distance entre les corps.
5.4.1 Calcul de la vitesse de libération
Comme nous le savons, si un corps a une vitesse suffisante, il peut quitter la Terre et se satelliser autour et ainsi adopter une trajectoire elliptique. Si on lui donne encore plus d'énergie, il pourra même quitter complètement la Terre et sortir de son champ de gravitation, sa trajectoire sera alors parabolique ou hyperbolique. Cette vitesse limite s'appelle vitesse de libération. Si la vitesse du corps est égale à la vitesse de libération alors, sa trajectoire sera parabolique.
Calculons cette Vitesse de libération. Il est très difficile d'intégrer les équations du mouvement de Newton. Un moyen beaucoup plus simple est de considérer l'énergie totale du corps. Elle découle directement de l'expression de la force de gravitation et de la 2ème loi de Newton.
L'énergie cinétique du corps est : 1/2mv2, son énergie potentielle est -GMp/R (où Mp est la masse de la planète ).
Questions :
Réponse :
L'énergie totale est 1/2mv2-GM/R. Elle est nulle à l'infini car v=0 et R=+ infini. Donc, en supposant que l'énergie est conservée le long de la trajectoire, il faut aussi qu'au départ, quand R=rayon de la terre, que l'énergie totale soit nulle. On en déduit V=(2GMp/Rterre)1/2. A la surface de la Terre, elle vaut ~11 km/s ! ! Pour le Soleil, elle est de ~42 km/s. Si un vaisseau doit quitter le Système Solaire, il doit d'abord s'échapper de la Terre (donc atteindre au moins 11km/s pour quitter la Terre) et ensuite atteindre au moins 42 km/s par rapport au Soleil pour s'en échapper ! ! Ces vitesses bien qu'élevées sont en fait réalisables. Les sondes Voyager et Pioneer sont toutes en train de quitter notre système Solaire, et ont donc acquis cette vitesse de libération.
5.4.2 Distance minimum des étoiles
Nous savons bien que les étoiles que nous voyons dans le ciel n'ont aucune influence (en tout cas négligeable) sur la dynamique de notre Système Solaire. C'est parce qu'elles sont beaucoup trop loin. Sachant que notre système Solaire fait environ 100 UA, calculer la distance minimale à laquelle une étoile de même masse que le Soleil doit se trouver pour que la force gravitationnelle qu'elle exerce soit au moins cent fois inférieure à celle du Soleil. (1UA=150 106 km).
Réponse : Du fait que la force de gravitation décroît comme le carré de la distance, pour être 100 fois plus faible, il faut donc être 10 fois plus loin. Donc l'étoile la plus proche est au moins à 1000 UA. C'est là en fait une bien faible estimation. En fait l'étoile la plus proche, Proxima du Centaure est à environ 4 années lumière, soit ~ 250000 UA ! !
Sachant que la Terre fait une révolution autour du Soleil en 1an et que la distance Terre-Soleil est ~150 106 km, calculer la masse du Soleil. On utilisera pour cela la formule établie par Newton de la vitesse moyenne de révolution: w =(GM/R3)1/2
Réponse : c'est une simple application numérique. La vitesse de révolution de la Terre est 2pi /(1 an) rad/s, que l'on nomme T. On a alors Ms=T2/G*R3. On trouve alors ~1030 Kg, ce qui est absolument gigantesque ! ! En fait, le Soleil à lui seul représente près de 99 % de la masse de tout le système solaire !
Un satellite en orbite géostationnaire autour de la Terre a une orbite circulaire calculée de façon particulière : il faut qu'il soit toujours à la verticale du même point autour de la Terre. Cela est très utile surtout pour les satellites de télécommunications qui ne doivent pas se déplacer par rapport au sol. En d'autres termes, leur vitesse de rotation autour de la Terre doit être la même que la vitesse de rotation de la Terre sur elle-même. Sachant que la masse de la Terre est 5.98 1024 kg, calculer cette distance.
Réponse : On utilise encore la même formule pour calculer la vitesse de rotation : w =(GM/R3)1/2 où ici M est la masse de la Terre. Omega doit être égal à la vitesse de rotation de la Terre sur elle-même, soit 2pi /(24 heures). On a alors R=(GM/w 2)1/3, on trouve alors ~36000 km.
5.5 Le retour de la comète de Halley
Newton, montra dans les Principia que les comètes pouvaient très bien être des petits corps suivant des orbites elliptiques très allongées, i.e. très excentriques, et à très longue période. Après un passage, la comète repart dans les confins du système solaire, mais elle devrait inévitablement repasser vers le Soleil au bout d'une période à peu près fixée. Ainsi, et contrairement à ce que l'on croyait à l'époque, les comètes ne sont pas des objets éphémères qui partent à jamais une fois disparus, mais bien des objets qui reviennent régulièrement dans le voisinage terrestre.
Halley prit la décision de dépouiller les archives astronomiques pour voir s'il pouvait identifier un objet avec une certaine périodicité. Il identifia une comète avec une orbite rétrograde qui apparût en 1682,1607 et 1531. Il fût cependant troublé que l'intervalle de temps ne soit pas exactement égal, comme le prévoit à priori la théorie de Newton. Mais il comprit rapidement que cela pouvait s'expliquer par des perturbations gravitationnelles éventuelles engendrées par les autres planètes du système solaire.
Avec l'aide d'autres astronomes français, il calcula l'orbite de la comète en tenant compte de l'influence gravitationnelle des planètes, et prédit qu'elle approcherait à nouveau du Soleil à la mi-avril 1759, plus ou moins un mois.
Ce fût une bonne prévision. C'est un fermier qui l'observa le premier le jour de Noël 1758, puis finalement, Charles Messier, trois semaines plus tard. La comète commença à contourner le soleil le 13 mars 1759. Ses caractéristiques orbitales étaient très semblables à celles calculées. Il ne faisait plus de doute que c'était bien là la même comète.
Halley ne s'était donc pas trompé, et la théorie de Newton remportait là son plus grand triomphe public.
L'oeuvre de Newton se répandit rapidement, et se posait à l'époque en complet contraste avec l'oeuvre de Descartes. Cette dernière propose la vision d'un monde complètement intelligible, où seule l'interaction directe entre les objets de l'univers peut engendrer leur évolution, leur modification. De plus, elle est non prédictive (mis à part un travail sur la propagation de la lumière) et avant tout qualitative. Newton, au travers de ses Principia, propose une approche complètement mathématisée, où la prédiction est enfin possible. Cependant, en dépit de son très grand succès, la découverte de Newton fut en butte à un certain scepticisme, en raison de la nature très mystérieuse de la force de gravitation. Certains virent dans celle-ci un retour au mysticisme, une régression vers les forces mystiques attractives répulsives, emphatiques etc. Newton lui-même n'apportait pas d'explication à la nature de cette force, qui agit de manière instantanée entre tous les corps (comme on le croyait à l'époque, mais on sait maintenant qu'elle se transmet à la vitesse de la lumière). En ce qui concerne la nature de l'espace-temps, l'approche newtonienne suppose qu'il puisse exister un temps et un espace absolu, et qu'il est possible de réécrire les lois de la physique dans un repère quelconque en appliquant la transformation de Galilée pour les trois dimensions d'espace, alors que le temps demeure inchangé (au mieux, un changement d'origine, ce qui n'a aucune importance). Enfin par un raisonnement simple, Newton avait supposé, étant donné la nature attractive de la force de gravitation, que l'univers devait être instable et s'effondrerait sur lui-même, ou au moins évoluerait de manière importante. En deux mots, l'univers devait avoir une évolution. Cette conséquence était très étonnante pour l'époque, et l'idée que l'univers puisse avoir une histoire et évoluer était incroyable. D'ailleurs Newton lui-même n'y croyant pas du tout, pensait finalement que c'était Dieu lui-même qui maintenait l'univers stable contre la force de gravitation.
Pour finir, on pourra se souvenir de cette très jolie phrase de Newton quand on lui demandait comment il voyait l'univers maintenant qu'il avait presque tout expliqué par la seule force de sa réflexion :
Je ne sais pas comment je peux apparaître au monde, mais pour moi-même, il me semble que j'ai seulement joué comme un enfant sur la grève, trouvant par chance, un plus beau coquillage, ou un galet plus lisse, alors que le grand océan de la vérité demeure encore inconnu devant moi.